141. Linked List Cycle
Question:
Given head, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.
Return true if there is a cycle in the linked list. Otherwise, return false.
Example:

Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).

Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.
Source code:
Version 1
Idea:
We can use unordered_set to detect if a list is cyclical.
When we go through each node one by one, we should records the reference of node (or memory address) in a unordered_set container. Every reference is unique, so if current node's reference is in the container, it means that a node had been visited in a list before, return true. If the current node is NULL, it's represented the end of the list and a cyclical list is invalid, return false.
Time complexity: O(n)
Space complexity: O(n)
1 | /** |
Version 2
Idea:
In order to reduce the space complexity to O(1), we can't declare any container to record the reference of node. Floyd's Cycle Finding Algorithm is quite efficient and simple.
What is Floyd's Cycle Finding Algorithm? wikipedia
When you want to solve the detection of multi-connected elements whether it's exist cyclical state, you can try to convert these questions to List structure, and List can be summerized into two parts:
Cyclical List structure
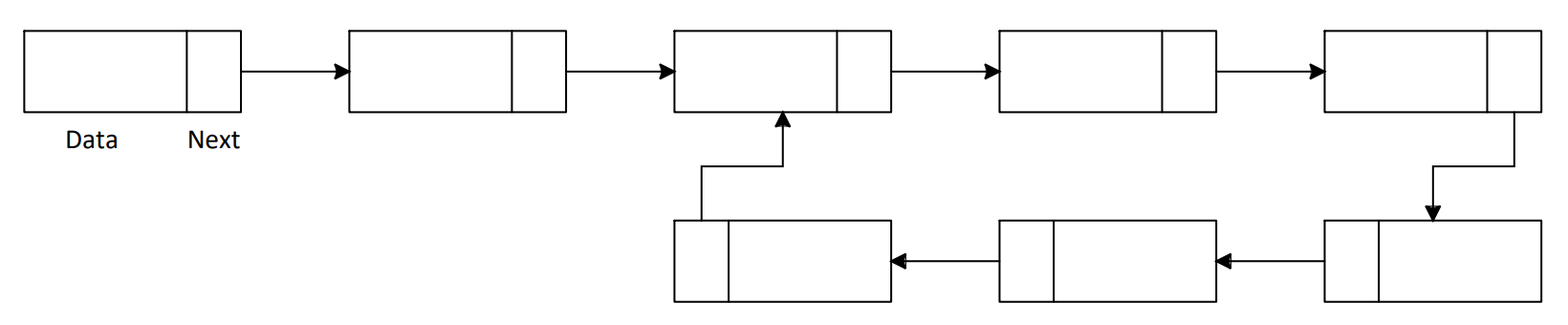
Non cyclical List structure

The algorithm is named after Robert W. Floyd, who was credited with its invention by Donald Knuth.
It is a pointer algorithm that uses only two pointers, which move through the sequence at different speeds. It is also called the "tortoise and the hare algorithm".
How does it work?
Declare two variable as a slow pointer and a fast pointer. The slow pointer moves one step at a time while the fast pointer moves two steps at a time.
If there is a non cyclical List, the fast pointer will reach the end first and the last node points a NULL, you can return false in this case.
If there is a cyclical List, the fast pointer will eventually meet the slow pointer, so you can return true at 18 line.
Time complexity: O(n)
Space complexity: O(1)
1 | /** |